Lens prior matching with
latent diffusion models

SKACH winter meeting 2025

2024/27/01, ISSI Bern
contact_qr.png Philipp Denzel, Y. Billeter, F.-P. Schilling, E. Gavagnin @ ZHAW
L. Stanic, G. Piccoli, T. Doucot, M. Bussmann, P. Saha @ UZH

Strong gravitational lens prior

illustration_quasar_lensing_ska.jpg
Credits: NASA/ESA

  • Let \(D\) be a lens observation
  • We want to model the lensing galaxy \(\Gamma_i\)
  • In Bayesian terms: \(\ p(\Gamma | D) \propto p(D | \Gamma)\ p(\Gamma) \)
    • data likelihood \(p(D|\Gamma)\) contains the physics
      \(p(\Gamma)\) is our prior knowledge about galaxies
  • This means finding a galaxy s.t.
    \(\quad\quad \Gamma_i = \arg\max\limits_\Gamma\ \ p(D|\Gamma) + p(\Gamma) \)

Strong gravitational lens prior

real_gal-inv.png

Figure 1: Mandelbaum et al. (2014)

Map-to-map translation

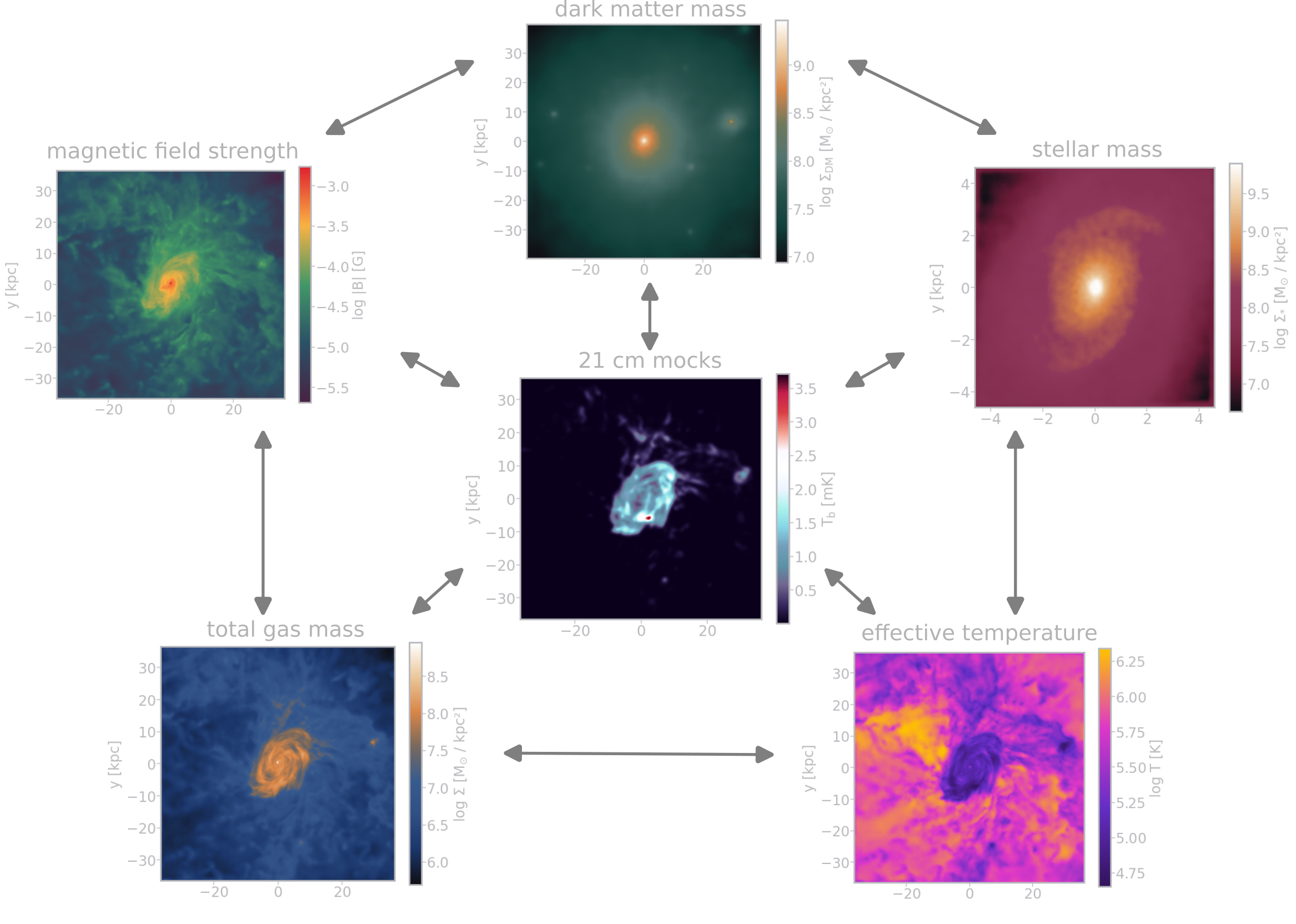
domains_directions.png

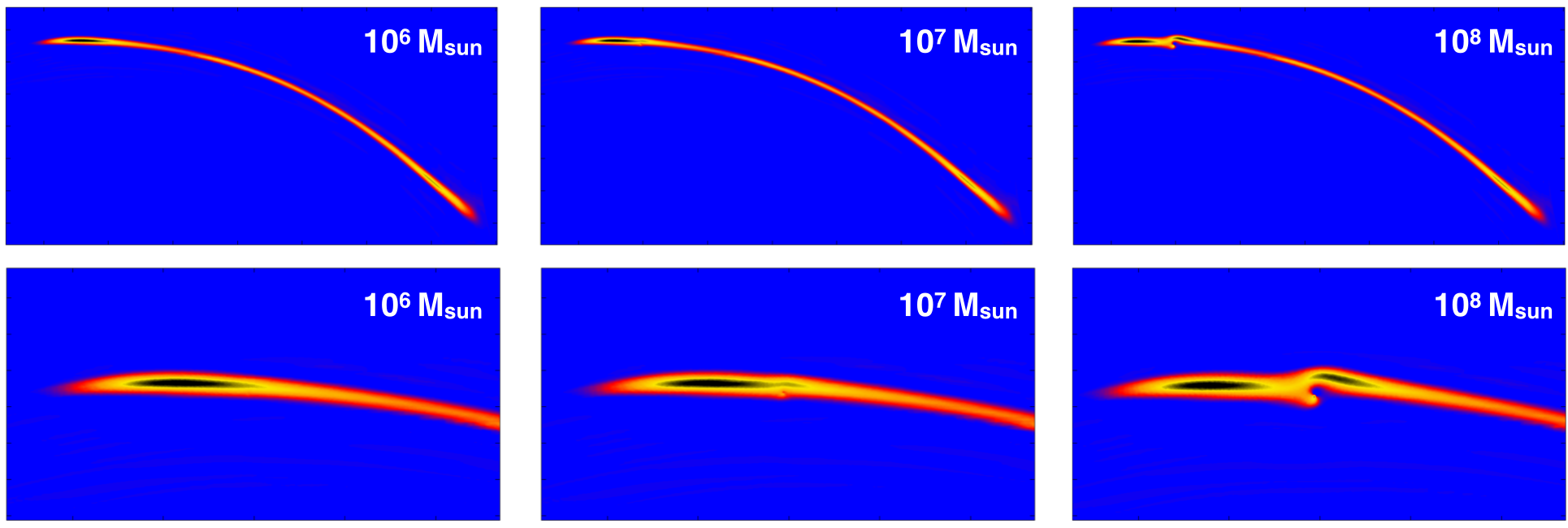
Figure 2: Denzel et al. (2025, in prep.)

Generative deep learning for galaxies

  • Recent work:
    • map-to-map translation of simulated galaxies
  • Roadmap to a physical & plausible lens models:
    • Physical model: map-to-map translation models
    • Sampling halos: (random/guided) generation
    • Applications to observations

Deep generative models

  • match some data distribution \(p(x)\) with a neural network \(p_\theta(x)\)
  • our models are trained on simulated galaxy samples \(\Gamma_{i}\)
    • caveat: each simulation implements a specific feedback model \(\phi\)
  • unconditional generation of galaxies \(g\):
    \( g \sim p_\theta(\Gamma | z; \phi) \quad \text{where}\quad z\sim\mathcal{N}(0,1) \)
  • conditional generation of galaxies \(g\) including some information \(c\):
    \( g \sim p_\theta(\Gamma | z, c; \phi) \)

Which generative model?

  • depends on use case… for strong gravitational lensing we need:
    • efficient, fast, good distribution coverage
    • optionally choose Einstein radius
  • DDPMs: ideal, but too slow
  • GANs: difficult to train
  • VAEs: in latent space, but poor quality
  • Compromise: all of them

Latent diffusion

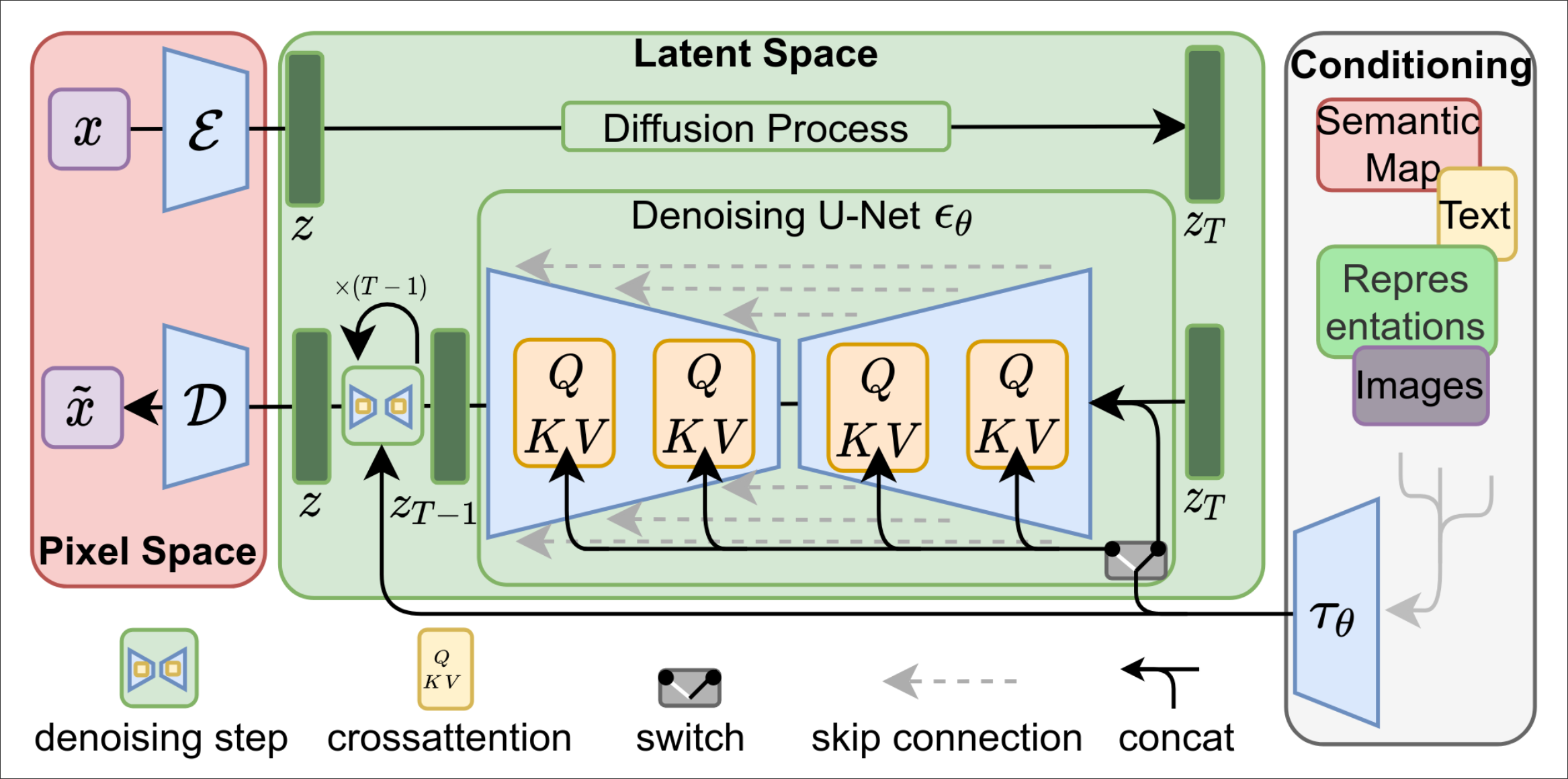
latent_diffusion.png

Figure 3: Latent diffusion by Rombach et al. (2022)

Key ingredient

Key ingredient

Regularization of the latent space

Regularization of the latent space

Diffusion

Current status

  • basic VAE version is trained
    • regularization of latent space is difficult…
  • results need fine-tuning, more elaborate objective
    \(\mathcal{L}_\text{VQGAN} = \mathcal{L}_\text{L2} + \mathcal{L}_\text{KL/VQ} + \mathcal{L}_\text{PatchGAN} + \mathcal{L}_\text{LPIPS}\)
  • some samples from recent VAE trial runs:

ldm_vae_2412_1.png

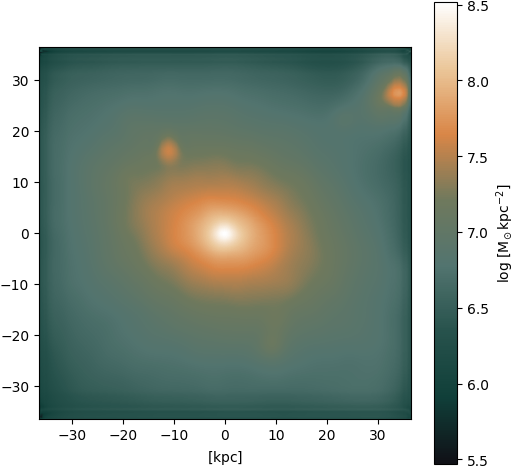
ldm_vae_2412_2.png

ldm_vae_2412_3.png

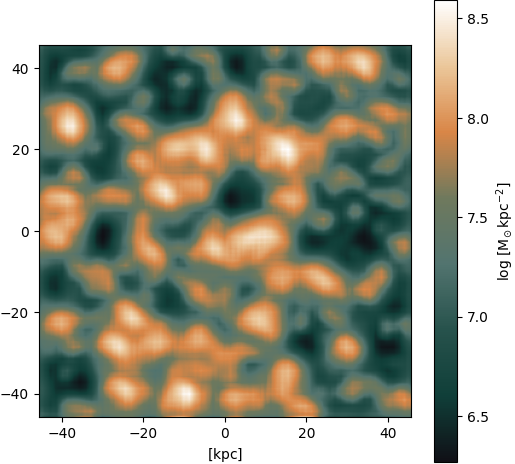
ldm_vae_2412_4.png

Application: Strong gravitational lensing

A lens with an interesting history

  • The "polar" quad (time delays without seasonal gaps)
  • First discovered in Gaia D2: Lemon et al. (2018)
    • as a quadruply imaged quasar
  • Confirmed PDLA by Lemon et al. (2022)
    • Proximate Damped Lyman-\(\alpha\) Absorber quasar

zig_zag_gaia.png
Lemon+ (2018)

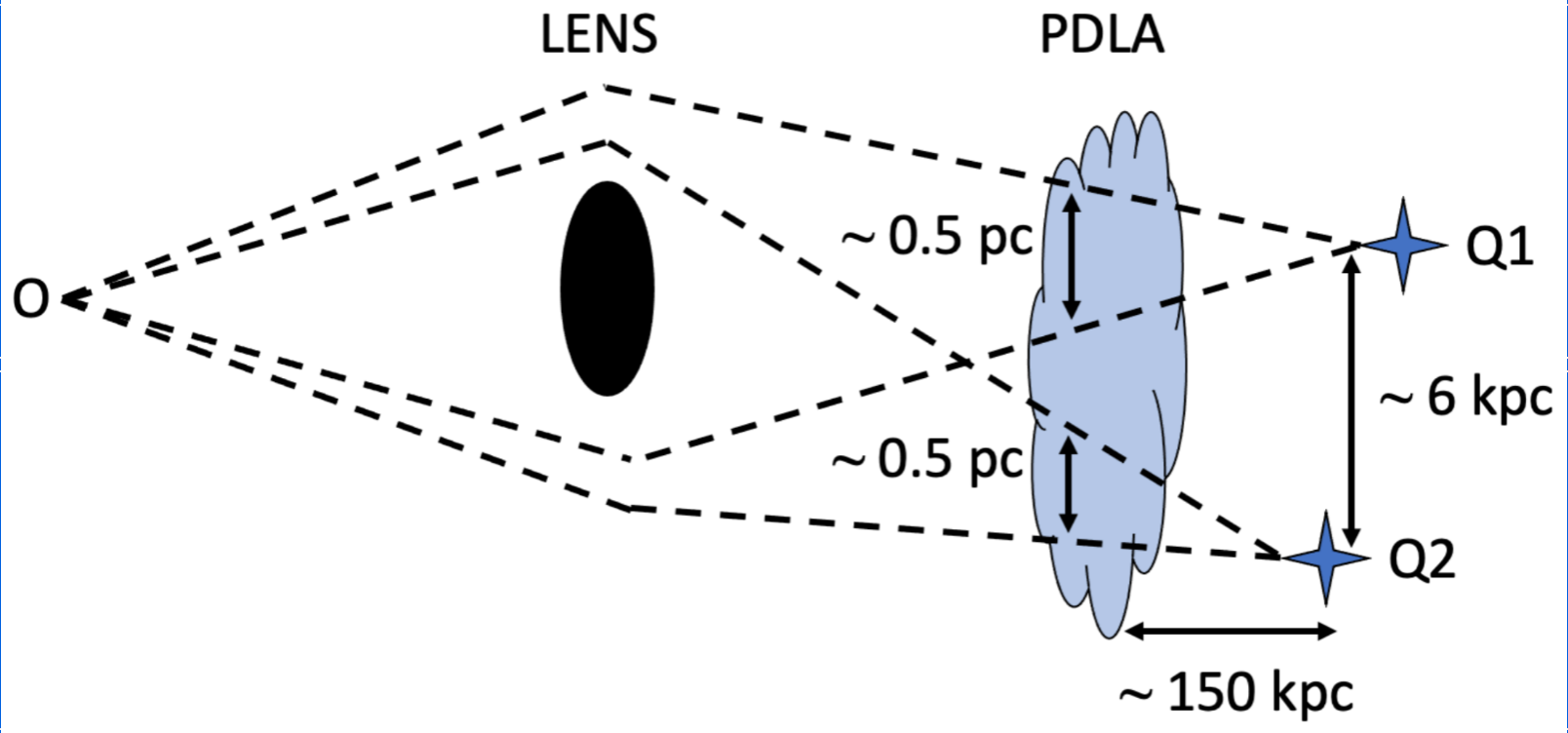
zig_zag_pdla.png
Lemon+ (2022)

Zig-zag lens

zigzag_lens.png

Figure 5: Dux et al. (2024)

Zig-zag lens

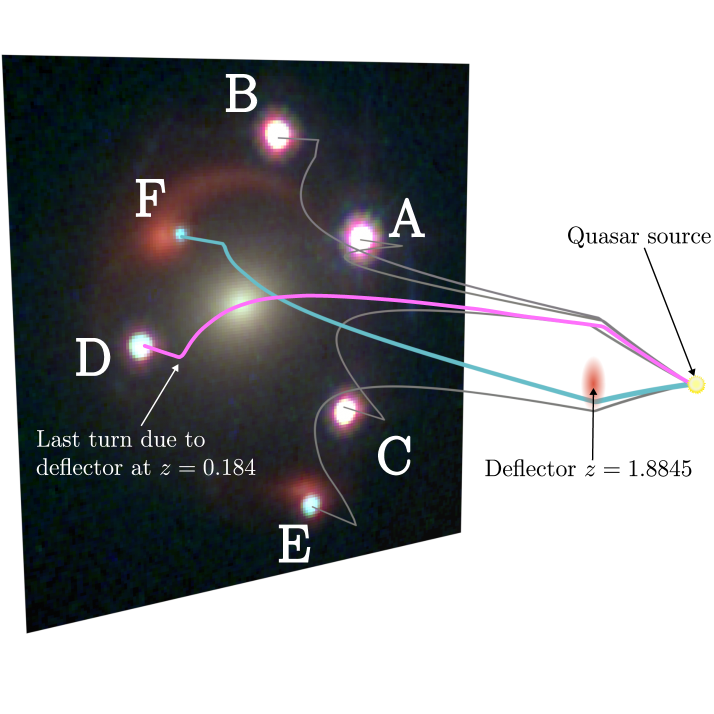
zigzag_trace.png

Figure 6: Dux et al. (2024)

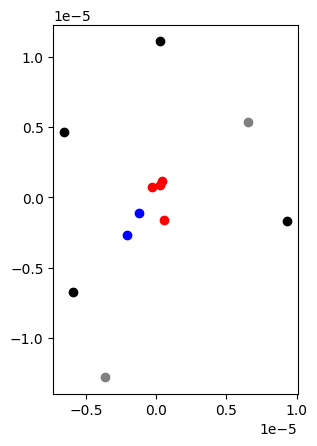
Zig-zag lens model

  • Brute-force trial matching
  • Raytracing and lens matching by UZH group
\begin{equation} \begin{aligned} x_1 &= D_{01} \, \theta \\ x_2 &= D_{02} \, \theta - D_{12} \, \hat\alpha(x_1) \\ x_3 &= D_{03} \, \theta - D_{13} \, \hat\alpha(x_1) - D_{23} \, \hat\alpha(x_2) \end{aligned} \end{equation}

ezigzag_first_plane.png

Summary: Importance for SKA?

  • Good preparation for what's to come…
  • VLBI & SKA-MID: Band 2/5/6
    • extended AGN jets on sub-parsec scales
    • CO (1–0) maps (Band 6 ~ ALMA scales)
    • sub mJy/beam arcs (\(\approx\) 5 mas) → nature of dark matter

dm_models_mckean15.png McKean et al. (2015)

radio_gl_hartley19.png
Hartley et al. (2019)

Created by phdenzel.