Albert and Grant - A Tale of Triangles
by Philipp Denzel and Prasenjit Saha
In one of Einstein's notebooks from 1912, there is a curious figure with an even more curious caption.
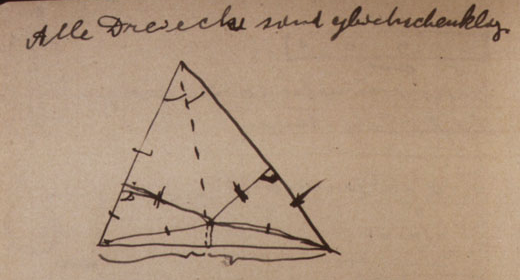
The caption (in German) reads Alle Dreiecke sind gleichschenklig meaning All triangles are isosceles.
We guess a few historians of science have stared at the remark, shaken their heads in disbelief, and moved on. On the other hand, if you happen to have Grant Sanderson's video How to lie using visual proofs fresh in your mind, the sketch will look suspiciously familiar. There's no doubt, Albert and Grant are talking about the same fake proof!
Here we'll explain, with the help of some interactive graphics, a mathematical sleight-of-hand hiding in Einstein's sketch. Spoiler alert: it will give away a punch line from the video.
Start with a triangleHere's a triangle. You can change it by dragging any of the vertices. Try it now! (If you drag a vertex outside the panel and can't get it back, just refresh the page.) If you have JavaScript disabled, you should see some static figures below. Our explanations will still work with those. |
|
Two lines and their intersection pointNow we draw two lines. One is the angle bisector at one of the vertices (doesn't matter which one). The other is the perpendicular bisector of the side opposite said vertex. As you can verify by altering the triangle, two lines coincide if the two sides (not the bisected one) have equal length. Otherwise they will intersect at some point (say P). As we can also verify, P will lie outside the triangle. Verification is not mathematical proof, of course. But proof will follow. |
|
A few more linesFrom the intersection point P we now drop perpendiculars to the remaining sides of the triangle. If a side is too short to reach the relevant perpendicular, we just extend the side as needed. Then we join the point P to the remaining two vertices of the original triangle. Our construction is now complete. |
|
|
A little detail, which you can ignore: we have used two different line styles for our constructions. All solid lines simply join two points that are already known. For the dotted lines you have to solve for a point. (Before computer graphics, the former kind needed just a ruler, the latter kind needed a ruler and a compass.) |
|
Some congruent triangle pairsWith all the perpendiculars we have drawn, there are several right-angled triangles in our construction. All of them have the intersection point P as one of their vertices. Let us consider the triangles in pairs (shown in turn in green). First, there are the triangles involving our original angle bisector and the perpendiculars we dropped from P. They have the bisector line itself in common, the bisected half-angles are equal, and each also has a right angle. So these two triangles are congruent. They are also mirror-images of each other, sharing one side. Then, there are the two triangles involving the perpendicular bisector we drew. They have the bisector itself as a common side, and the bisected sides are equal, and both are right-angled triangles. So again these two triangles are mirror-image congruent triangles. |
|
|
Now consider the intersection and gap formed when we switch between the above two triangle pairs. These are yet two more right-angled triangles, because each includes one of the perpendiculars we drew. They also share two congruent sides with the above two congruent pairs. Ergo these two triangles are congruent. These are not mirror images, but rotated versions of each other. |
|
|
One of these green triangles is partly inside the original triangle, one is completely outside. Together they show the difference between the original triangle and an isosceles triangle. You can make make the original triangle isosceles by transferring some length from one leg to the other, and the triangles show you how much. |
|
A sleight of handAs we have seen, the intersection point P of the angle-bisector line and the perpendicular bisector lies outside the triangle. You can make P appear to lie inside the triangle, by drawing a fake angle bisector. (You could also fake the perpendicular bisector, but that's easier to spot.) With a genuine perpendicular bisector, the first pair of congruent triangles is still congruent. |
|
|
The other two pairs of triangles, though they're still right-angled, are not congruent any more. (Unless you make two sides equal.) The fake angle bisector we used to put P inside the triangle breaks the argument. . . |
|
|
. . . which is just as well, because otherwise we'd have proved all triangles to be isosceles! |
|
In the background
Einstein's sketch and caption isn't on some random piece of paper of doubtful authorship. It appears next to what is now a textbook calculation in astrophysics, and the notebook page is well known to historians of science.

It is about an effect that happens when two random stars at different distances from us happen to nearly align along the line of sight. The light from the more distant star gets focused by the gravitational field of the less distant star, resulting in a characteristic apparent brightening over a period of days or weeks, according to the formula Einstein derives here. It very rarely happens, and you have to monitor millions of stars to pick out this effect from all the other ways the apparent brightness of stars can change. In Einstein's lifetime it was only a theoretical curiosity, but in the 1990s observing gravitational lensing by stars (and later even exoplanets) became feasible. Surveys like OGLE nowadays routinely discover exoplanets this way. The gravitational lensing phenomenon also applies to galaxies, and on that topic there is even some research by the present authors.
What prompted Einstein, in the middle of solving the riddles of the universe, to work through this fake proof? Was he solving a little brainteaser from a newspaper while waiting for a train? Was he preparing a lecture on how to lie with visual proofs? Maybe there is a clue somewhere else in his notebooks. Or maybe we'll just never know.